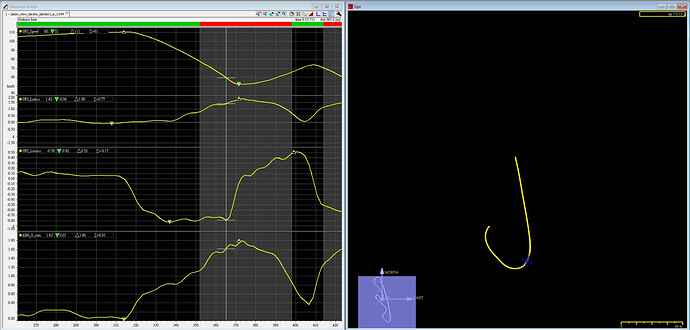
This is the data from my friend, who is the record keeper on this circuit with his Rotax Max senior 125 mount on a rear brake only chassis.
Please look at the data of the cursor place. LonAcc is very close to the limit 0.8g, but there is LatAcc 1.42g combined. As I know, when the rear brake force is close to the grip limit, the rear will slide if we turn the steering. So how do we explain this situation?
I think we aren’t understanding question. What is the contradiction you see. Can you explain?
How does it compare to other laps at this point. My first thought it’s that it’s a bump.
0.8g is the maximum decerelation on the straight line, which means all the grip of rear tyres contributes to decerelate. How can he turn in this corner and request more grip from the rear tyres and it won’t slide?
In fact , my data is almost the same in this corner. But I am sure I make my turn in and trail brake after heavy braking intentionally. So my question is more about the kart dynamic or physics.
They are all the same. I am sure there is no bump.
The driver hits maximum braking ability at the 0.8g, but the kart is also slowing down during that phase, so the kart’s ability to corner grows as the kart slows down, because you are asking less of the tire’s traction ability.
If the driver were to attempt to turn hard and load the kart laterally while the kart was still at high speed, with heavy brake pressure on, it would begin to slide. But the driver appears to be loading the kart laterally about halfway into the braking zone, so has slowed down about 20 km/h. At this point the kart is better able to cope with lateral load, because the speed has decreased and the tire needs less grip to change direction at a slower speed.
Or at least that’s how I see it.
Slip angle maybe? There’s grip and there’s slip angle which is it’s stretched state.
I’m not saying any of this is 100% right, but just something to consider…
I would think of this as “all of the AVAILABLE grip of the rear tires contributes to deceleration.”
The rear tires have the capacity for way more potential traction, but their actual available grip is limited by the load they are carrying. With rear brake only karts, when you brake, you transfer load from the rear tires to the front, but you need load on the rear tires to generate traction for deceleration; so essentially the result of what you are doing (braking) reducing the rear tires’ ability to produce the thing you want (deceleration).
When you add steering input, you mechanically ‘jack’ load from the inside front tire to the outside rear tire; so you’re simultaneously asking the rear tire for more of it’s maximum potential traction, while providing it with the load it needs to produce that maximum potential traction. However, when doing this it is very easy to ‘shock’ the rear tire (get the load provided vs traction requested balance out of sync), which can cause the tire to lose traction. Therefore, it is especially critical during the initial application of steering inputs that they be done with a very delicate touch, and that the turning be timed in a way that provides that critical balance of not asking for more traction from the tire before you provide the load required to support it. One way to think of it is that you need to give the initial load you provide the time it needs to get the tire ‘stretching’ towards it’s traction potential.
You are basically pulling back a few layers of physics here. I’m going to simplify this to basic thoughts and equations.
First, the .8g’s are in one direction (vector) when braking. As the kart slows, and you lift the brake pedal in preparation of the turn, the acceleration is slowing. Since mass of the kart stays the same, the acceleration is decreasing and therefore the tire force decreases. It is not using the maximum amount of grip (F=ma). Also when the turn is initiated, you’re dividing weight between front and rear tires
Second, the lateral acceleration is where things get more complicated. This will layer on variables such as weight transfer, tire construction, slip, yada yada yada. A better way to think of this is from the force of friction formula. Force of friction = friction coefficient x normal force. To increase grip, we need to increase the force of friction. The friction coefficient stays the same (compound) but your force is dramatically increased on the outside tires (yes, front and rear) due to weight transfer. This is why you can see increased g’s in cornering in karting and other motorsports as well.
There are a lot more forces at work but those are two easy ones to start with. You can test the force of friction equation in a kart as well. Let’s say we get .8’s in braking force. Top team drivers are very good at active karting and will push on the wheel or the foot pegs into a braking zone. This is to weight the back tires to increase the force of friction and maybe produce .85g’s of braking force.
This seems very high tech for karting!
Not saying you won’t learn from the above data in regards to slip angles, braking and what not, but sometimes over analysing data can get you more confused than what it’s worth.
Just my two cents.
After thinking these few days, I derived a equation about Possible Max GPS_LonAcc. It works fine:
sqrt((GPS_LatAcc*0.55)^2+GPS_LonAcc^2)
where 0.55 is the weight distribution percentage of the rear tyres and it should be edited according to real number by measruring.